Curriculum Innovation, Testing and Evaluation: Proceedings of the 1st Annual JALT Pan-SIG Conference.
May 11-12, 2002. Kyoto, Japan: Kyoto Institute of Technology.

An application of a many-faceted Rasch model to writing test analysis

by Yuji Nakamura (Tokyo Keizai University)


Theoretical background and rationale
"Finding a rating method that is practical, reliable, and statistically well-founded is a problem for many writing teachers."

What is the best way to assess writing compositions? Rudner (1992) points out that it is best to have multiple raters assess all compositions within a given group. When multiple raters are involved, however, a score adjudication process is often needed to resolve rater discrepancies. In such cases, often third-rater adjudication may be used to correct excessive disparities.
Practically speaking, however, it is often difficult to find multiple raters (usually peers) to evaluate all compositions. Therefore, teachers generally either evaluate compositions by themselves (a less reliable method), or else employ multiple choice grammar tests (a less valid method) to assess writing. Finding a rating method that is practical, reliable, and statistically well-founded is a problem for many writing teachers.
This paper focuses on one way of using Rasch analysis in assessing essay writing performance. The goals of the study are:
  1. to establish an effective arrangement of multiple raters to measure students' writing ability, and
  2. to reduce the rater workload by paring in an organized, and statistically reliable way.
Research design and method

Thirty-two Japanese college students took a writing test consisting of a composition on an open topic. The compositions were then rated according to seven criteria on a four-point scale. Four raters worked in various combinations to form six pairs. Rater responses were analyzed using a many-faceted Rasch measurement (FACETS) model. Details concerning the research method are summarized below:
Task: Students wrote a composition on a single topic they chose within a 40 minute period in class.
Raters: 4 raters (Rater A, Rater D, Rater M, Rater Y)
Pairs: 6 pairs (AD, AM, AY, DM, DY, MY)
Rater Coverage: Each student composition was evaluation by two raters.
Note 1: Discourse = Logicality, Fluency = Ease of reading (based on word length and accuracy), Content = Originality, Overall = A holistic, general impression
Note 2: Sentence length was not measured per se in this study, though it might have affected raters' judgments.
Rating scale: 4-point scale (1=poor, 2, 3, 4=good)
Subjects: 32 Japanese university undergraduate students

[ p. 171 ]


Acceptable ranges for the infit and outfit statistics in the performance test were 0.6 - 1.4 (The items below 0.6 were included in a special category called "overfitting" and those above 1.4 were labeled "underfitting", while all items outside this range were categorized as "misfitting.")
Each composition was assessed by two raters. Each of the raters read 16 compositions, comprising half of the total volume. The 32 compositions were arranged into six piles of 5 or 6 compositions and each rater was assigned to tackle three different piles. In this way, each pile was assessed by slightly different paired raters.

Brief explanation of Rasch modeling and logits

Since Rasch modeling deals with an assumed single underlying trait which enables us to place both items and persons on the same continuum, we can analyze data about individual ability and item difficulty unidimensionally on a single scale. Furthermore, in production tests such as writing tests, the raters' severity or harshness can also be examined by logit calculation.
The range of student ability and item difficulty in this study both showed a spread of about 6 logits. A logit is a way of expressing the probability or odds of a particular event, outcome or response and is short for 'logistic probability unit' or 'log odds unit'. The units on the scale of probability used in reporting the results of IRT analyses are called 'log odds units' or logits (cf. Davies et al., 1999).

Purpose of the research

The purpose of this research was to determine the extent paired composition assessment ratings could reduce a raters' workload without loss of statistical rigor. In other words, the research question was, "Do all teachers need to evaluate all students' compositions individually for maximum statistical rigor?" The following sub-questions were answered through many-facet Rasch measurement analyses:
  1. How well did the seven rating categories function?
  2. What was the relationship among the three facets (students, items, and raters)?
  3. What was the degree of rater severity/leniency?
  4. How widely did student ability differ?
  5. How widely did the item difficulty differ?
  6. How effective was this paired rating system?
Results and discussion

Sub-Question 1: How well did the seven rating categories function?

Table 1 shows that 4 of the 7 rating categories (1=poor, 2, 3, 4=good) functioned well in measuring these students, which is evident especially in the Outfit Mean Square and Calibrations Measure columns. In other words, all the outfit mean squares (.8, .9, 1.0, 1.1) were within the acceptable set range, and the calibration measures rose smoothly along with the rating category (-1.42, -40, 1.37, 3.80). Thus Sub-Question 1 was answered positively: many categories in this study worked well.

[ p. 172 ]


Table 1: Category statistics
Data Quality Control Step Calibrations
Category Score Counts Used % Cum. % Average Means Exp. Means Outfit Mean Square Measure S.E.
1 12 3% 3% -1.42 -1.21 .8
2 94 21% 24% -.40 -.33 .9 -2.85 .31
3 232 52% 75% 1.37 1.33 1.0 -.49 .14
4 110 25% 100% 3.80 3.82 1.1 3.34 .15

Sub-Question 2: What was the relationship among the three facets (students, items, and raters)?

Table 2 gives us a bird's eye view of three facets of this study: students' ability, raters' severity, and item difficulty). The raters varied significantly in their degree of harshness. Also, the range of student ability was quite wide, ranging from nearly 5 to -1. Among the seven categories in this study, grammar was the most difficult, while content and vocabulary were the easiest. The overall ratings (a comprehensive general category) tended toward the mean. This is hardly surprising it gives a more or less general view of the other items and does not provide such specific information.
When we look at the order of these items, grammar items were easiest to determine and most severely judged. This is probably because it is easy for the raters to decide what is correct and what is not correct, and they naturally tend to be harsh. On the other hand, content items were rated most leniently, perhaps because the originality and creativity intrigued raters from an emotional point of view. Also, when we examine vocabulary items, if students chose novel words, or used even one convincing word, they tended to get good scores. Hence we can say that vocabulary items were rated rather leniently. Thus, in Sub-Question 2 the facets in this study displayed an interesting and complex relation.

[ p. 173 ]


Table 2: All facet vertical "rulers"
Table 2

[ p. 174 ]

Sub-Question 3: What was the degree of rater severity/leniency?

The statistics column in Table 3 shows that there were no misfitting raters. All raters functioned within the acceptable range (0.6 - 1.4), which is usually applicable to writing and speaking performance test rating scales. In other words, the data from this study suggests that inter-rater reliability was high. As we notice in this table, harshness or leniency, which is shown in the Measure column does not affect the fit statistic. One possible explanation for this is that instructors who taught these students may be more familiar with what they intended to say, even if their writing samples were muddled. Thus, Sub-Question 3 revealed that although the degree of harshness/leniency varied considerably among raters, the combined inter-rater reliability was within acceptable parameters.

Table 3: Raters' measurement reports (arranged by N)
Observed Score Observed Count Observed Average Fair-M Average Mode Measure S.E. Infit MnSq Z Std Outfit MnSq Z Std ? N raters
309 112 2.8 2.85 -.76 .17 .9 0 1.0 0 Rater A
314 112 2.8 2.79 -.99 .17 .9 .17 .9 0 Rater D
365 126 2.9 2.98 -.22 .16 1.1 0 1.1 0 Rater M
348 98 3.6 3.54 1.97 .23 .7 -1 .9 0 Rater Y
334 112 3.0 3.04 .00 .19 .9 -.6 1.0 -.1 .38 Mean (Count: 4)
23.4 9.9 .3 .30 1.17 .03 .1 .9 .1 .5 .03 S.D.

RMSE (Model): .19 Adj S.D.: 1.15 Separation: 6.11 Reliability: .97
Fixed (all same) chi-square: 116.0 d.f.: 3 significance: .00
Random (normal) chi-square: 3.0 d.f.: 2 significance: .22
Sub-Question 4: How widely did student ability differ?

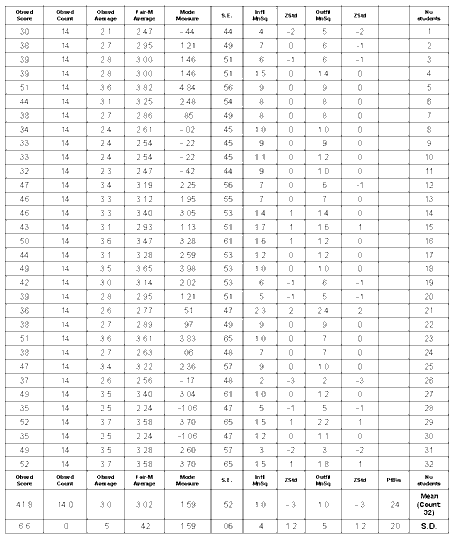
Table 4 informs us of student ability. Student 5 was the most able, while 28 and 30 were the least. Concerning misfitting students, we might want to look into numbers 15, 16, 21, 29 and 32. Especially student 21 should be examined in detail because of the misfitting scores (mean of squares 2.3 - 2.4). Also, we might want to examine overfitting students such as 26 and 31, though overfitting students did not affect the statistical data as much as underfitting students.
Some of the misfitting students can be explained in terms of their unexpected response patterns. Let us take a look at these in Table 5.

[ p. 175 ]

Table 4: Students' measurement reports (arranged by N)
Table 4
RMSE (Model): .53 Adj S.D.: 1.50 Separation: 2.85 Reliability: .89
Fixed (all same) chi-square: 296.0 d.f.: 31 significance: .00
Random (normal) chi-square: 30.9 d.f.: 30 significance: .42

Continue to Part 2


2002 Pan SIG-Proceedings: Topic Index Author Index Page Index Title Index Main Index
Complete Pan SIG-Proceedings: Topic Index Author Index Page Index Title Index Main Index

[ p. 176 ]

Last Next